三角形 比率 定理 126170-三角形 比率 定理

 三角形と平行線の線分の比 まずは 三角形と平行線の線分の比の ルールを覚えましょう。 ポイントは ①2つの辺が平行であれば ②どの辺の比の関係が成り立つのか を押さえる というところになります。直角三角形の直角の対辺を斜辺という（図 4）。斜辺は、直角三角形の 3 つの辺の中で最も長い。 斜辺を除く残りの 2 辺のことを、直角をはさむ 2 辺と呼ぶ。 直角をはさむ 2 辺 a，b と、斜辺 c の間には、次の関係が成り立つ（ピタゴラスの定理）。 a 2 b 2 = c 2 三角形で、3 辺 a，b，c の長さ三角形と比 三角形と比 三角形の一辺に平行な直線をひいた時にできる線分の比 について考えていこう。 辺AB を 4等分 するように 点D、E、F をおいてある。 直線は 3点 から 辺BC に平行になるようひいてあるよ。 AD：DE：EF：FB＝1：1：1：1 となっている

1

三角形 比率 定理

三角形 比率 定理- まとめ：直角三角形の比3つを使い倒せ！ 中学数学でよく使う直角三角形の比は次の3つ。 30、60の直角三角形 45の直角三角形 3 4 5の直角三角形 これを覚えるだけで三平方の定理を使わなくてよくなるから、 だいぶラクになるね。 いきなり覚えるのは中点連結定理とは、要は「相似比が1：2の三角形」と理解すればいいです。 三角形の中点を結ぶことによって、相似の三角形を作ることができ、相似比が1：2になるというわけです。 辺の中点なので、相似比が1：2になることは容易に理解できます。 この

直角三角形面积一定它的两条直角边的长度成什么比例 扒拉扒拉

  ピタゴラスの定理を使って、良い比率の三角形を無限に生み出す 数学 Tweet Pocket ピタゴラスの定理（または三平方の定理）は、誰もが小学生や中学生の頃から知っている馴染み深い定理だろう。 ピタゴラスの定理を使って「3対4対5」など三辺の例 (1) 1 2 x 斜辺がxなので 1222=x2 x2 = 5 x > 0 より x= 5 (2) x 12 13 斜辺が13なので x2122 数学Iの三角比の授業から。 今日は、3辺の長さから三角形の内接円の半径を求める問題。 教科書はいきなり内接円の半径を求める問題になっている。 教科書の解答は次のような流れだ。 1．余弦定理を用いてcosを求める。 2．三角比の相互関係を用いて、sinを求まる。

 定理：三角形 a b c abc a bc の内接円と辺 b c bc bc の接点を d d d とおく。 d d d から辺 b c bc bc と垂直な直線と内接円の交点を e e e とおく。さらに a e ae a e と b c bc bc の交点を f f f とおくとき， b d = c f bd=cf b d = cfガウスの驚異の定理（ラテン語：Theorema Egregium）は、曲面のガウス曲率が曲面自身の上の長さを測ることから決定することができることを述べた定理である。実際、 第一基本形式 （英語版） (first fundamental form)の考え方の全体として理解され、第一基本形式とその一階と二階の偏微分とし三角形与三角学三角函数 三角函数 到目前为止，我们已经知道了三角形_角_之间的关系（例如，角的总和为180°）及_边_之间的关系（例如，毕达哥拉斯定理），但是没有任何东西将角和边的大小 关联 起来。 举个例，如果我们知道一个三角形的三条边，如何

ピタゴラスの定理を知らなくても この方法を「三四五（さしご）」と呼んで利用していました。 「三四五（さしご）」の起源は非常に古く、 ピタゴラスの定理が発見されるよりも以前、 4500年前のエジプトでは既に3：4：5の直角三角形を使っていたそうです。初等幾何学におけるピタゴラスの定理（ピタゴラスのていり、英 Pythagorean theorem ）は、直角三角形の3辺の長さの関係を表す。 斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は = が成り立つという等式の形で述べられる 。 三平方の定理（さんへいほうのていり）、勾股弦の定理（こう 手始めに、高さが同じ三角形の面積比の求め方を考えましょう。 三角形の面積は「（底辺）×（高さ）× 1 2 1 2 」でしたね。

利用三角函数知识证平行线分线段成比例

必杀 三角形44 与比例线段有关的几个定理共角比例定理及其证明 哔哩哔哩 Bilibili

 三平方の定理の公式を紹介します。下の図のように直角三角形の直角を挟む2辺をa,bとし、斜辺をcとすると a²b²=c² の等式が成立することを三平方の定理と言います。 三平方の定理の証明 三平方の定理の証明について紹介したいと思います。三角比（trigonometric ratio）是 三角学 的基本概念之一，指 三角函数 定义中的两线段的数量比。 定义 锐角三角函数 时，是指含此锐角的 直角三角形 中任意两边的比。  三角比・三角関数の公式一覧。 正弦・余弦・加法定理など このページでは、 三角比・ 三角関数 の公式 をまとめています。 予習・復習に役立てていただければ嬉しいです

北师大版九上数学4 2 平行线分线段成比例知识点精讲 腾讯新闻

威尼斯人www0com将此比值放到该平面中的三角形中去运算即可得证 威尼斯0com 官方注册

$15^\circ$ の三角比の値は覚えなくてもよいが、$15^\circ$ を含む直角三角形から導けるようにしておこう。 これらの角以外にも、$18^\circ$、$36^\circ$、$72^\circ$、$144^\circ$ などの角も、特殊な三角形を考えることによって三角比を 求めることができる。この証明は「相似条件とは？三角形の相似条件はなぜ3つなの？証明問題アリ」の記事でも詳しく解説しております。 スポンサーリンク 平行四辺形を作る 言い忘れてましたが、三角形と比の定理も 全く同じ方法 で証明ができます。 これが、冒頭で「この $2$ つの定理を区別する必要は メネラウスの定理という形では、1973年(昭和48年)から学校で教えなくなってしまいました（資料1 p136）。 平成に入った後しばらくして、類似のチェバの定理 *7 と共に03年(平成15年)実施の教育課程に基づいた07年(平成19年)度検定教科書で 完全復活 （資料2

三相似三角形的判定及性质 人教版高中选修4 1数学电子课本 数九网

1

尺规作图如何三等分一条线段 看完这个 不要再说你不会了

数学相似三角形知识点 相似三角形的性质和判定 星火网校

什么叫相似三角形

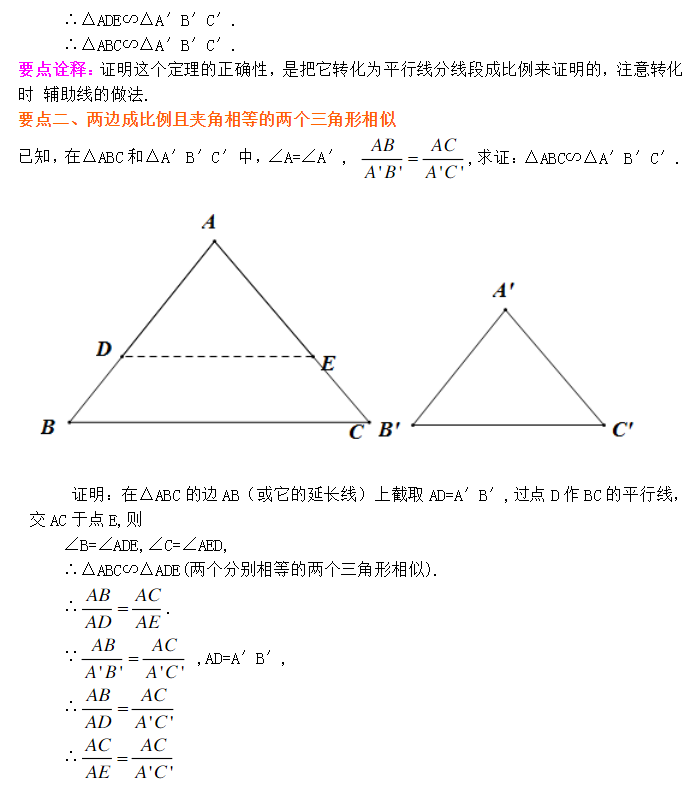
多重判定系数怎么求 北师大版九上数学4 5 相似三角形判定定理的证明知识点精讲 Yu Demon321 Mkq的博客 程序员宅基地

相似三角形相似三角形的判定和性质

相似三角形的性质及其判定定理是什么 星火网校

截距定理三角形thales定理 三角形png图片素材免费下载 图片编号 Png素材网

相似三角形判定定理 1 平行於三角形一邊的直線和其他兩 華人百科

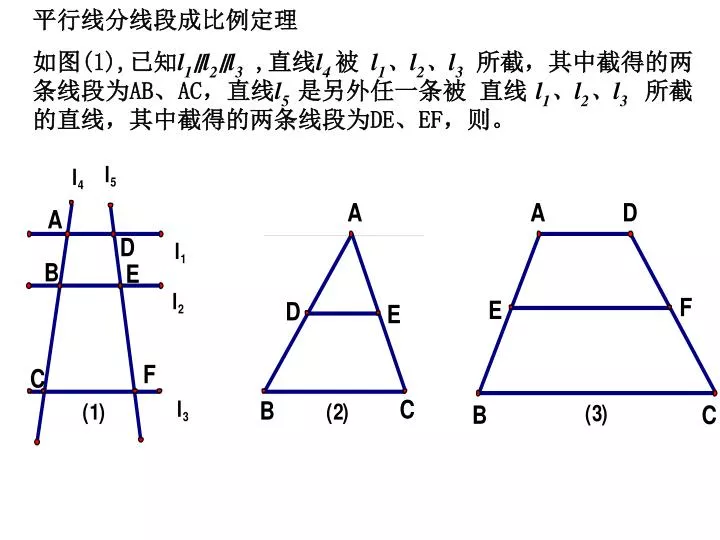
平行线分线段成比例定理 第二课时 初中数学教案 初中数学教案 中国教育资源网

预习 24 4 3 相似三角形的判定 小析初中数学 微信公众号文章阅读 Wemp

Amc10 数学中的面积公式推证

勾股定理 等边三角形 细品年立体几何高考题 勾股定理 三角形 直角 立体几何 高考题 手机网易网

中考數學重點 相似三角形知識點總結及模型分析 Itw01

0 4 几个平面几何中常见定理 知乎

几何课关于三角形你不得不记住的定理 从勾股定理到托勒密定理

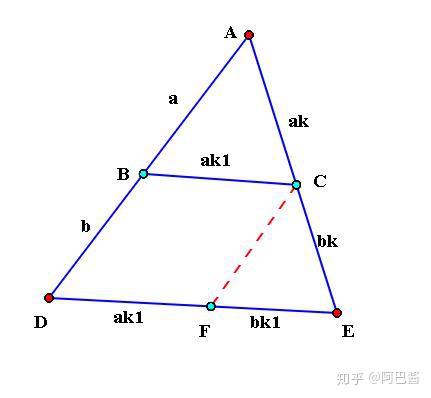
初中数学 相似三角形判定定理证明浅见 来说说你的方法吧 知乎

平面几何相关定理 静雅斋 51cto博客

02 相似三角形的性质 相似三角形的定理与圆幂定理高中数学 Youtube

直角三角形的相似關係 證明 Youtube

直角三角形三边比例 直角三角形三边比例关系 七月seo

多重判定系数怎么求 北师大版九上数学4 5 相似三角形判定定理的证明知识点精讲 Yu Demon321 Mkq的博客 程序员宅基地

01 相似三角形判定定理 相似三角形的定理与圆幂定理高中数学 Youtube

1

相似三角形的基本图及应用 Good

比例线段 相似三角模型比例线段

相似三角形判定定理 相似三角形判定定理 數學公式 相似三角形的性質定理 百科知識中文網

三角形比例线段定理

一个读起来比较拗口的定理 可能被你忽视了 每日头条

相似三角形判定定理 尚书坊

相似三角形对应边比例 相似三角形对应边成比例 这个是怎么证出来的 三人行教育网 Www 3rxing Org

几何课关于三角形你不得不记住的定理 从勾股定理到托勒密定理

初中几何 相似三角形的判定 定理知识点归纳总结例题讲解基础练 初中数学 学习资料大全 免费学习资源下载

必杀 三角形32 相似三角形巧用相似求比例 共边比例定理 哔哩哔哩 つロ干杯 Bilibili

直角三角形三边比例 直角三角形三边比例关系 七月seo

三角形中線問題與比例線段性質的應用 Isdp08am 隨意窩xuite日誌

初中 掌握這23個初中數學常用公式 數學成績輕鬆100 雪花新闻

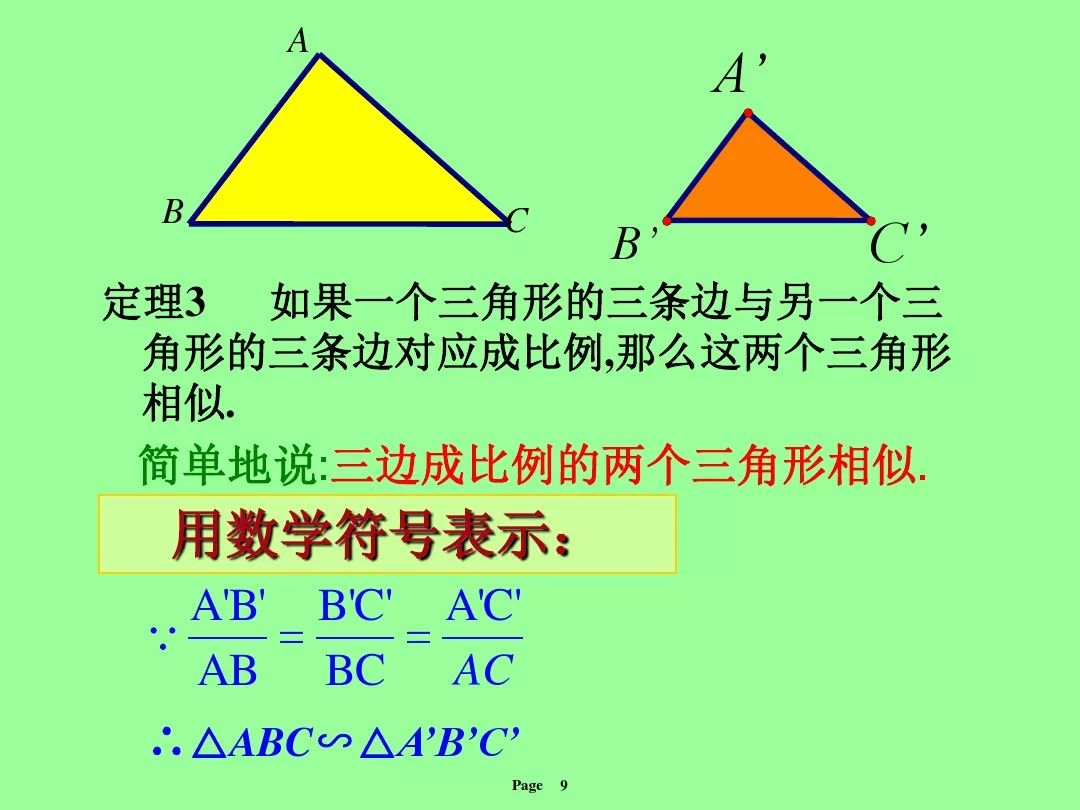
多重判定系数怎么求 北师大版九上数学4 5 相似三角形判定定理的证明知识点精讲 Yu Demon321 Mkq的博客 程序员宅基地

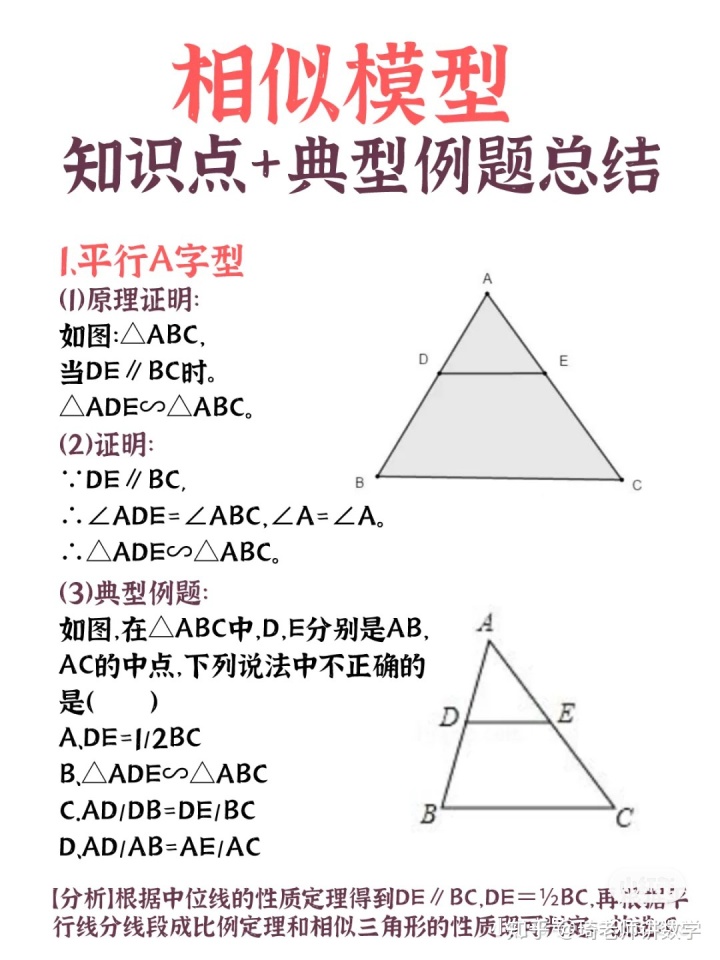
平行相似定理 初中数学 相似三角形模型合集提分收藏 阿诬123的博客 Csdn博客

初中数学相似三角形知识点 初三知识点总结 求学网

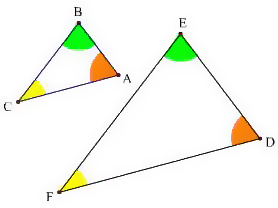
相似三角形 维基百科 自由的百科全书

30度60度90度勾股定理 30度 60度 90度的直角三角形三边的比例关系 朔旭金融网

三角形共边定理 西瓜视频搜索

怎么使用 相似三角形的定理 做证明题 一 百度经验

相似三角形判定定理的证明 图形的相似ppt下载 牛二ppt

第一章相似三角形定理与圆幂定理 人教版高中选修 B版 4 1数学电子课本 数九网

初中数学相似三角形的判定定理证明及利用三角形相似解决问题 每日头条

怎么使用 相似三角形的定理 做证明题 一 百度经验

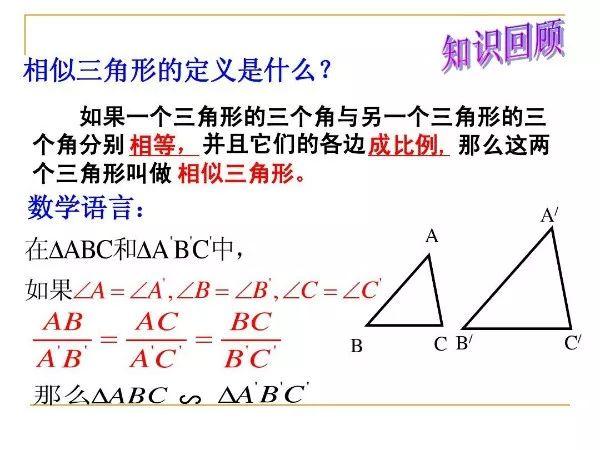
平行相似定理 初中数学知识点 相似三角形 Weixin 的博客 Csdn博客

相似三角形定理的证明

共角三角形 西瓜视频搜索

直角三角形斜边上的中点 扒拉扒拉

19年中考专题复习 相似三角形的存在性问题 三角形 定理 代数 新浪新闻

三角形相似的判定条件

二平行线分线段成比例定理 人教版高中选修4 1数学电子课本 数九网

1

相似三角形怎么判定 搜狗指南

必杀 三角形44 与比例线段有关的几个定理共角比例定理及其证明 哔哩哔哩 Bilibili

相似三角形知识学习归类 学起来真轻松 每日头条

直角三角形面积一定它的两条直角边的长度成什么比例 扒拉扒拉

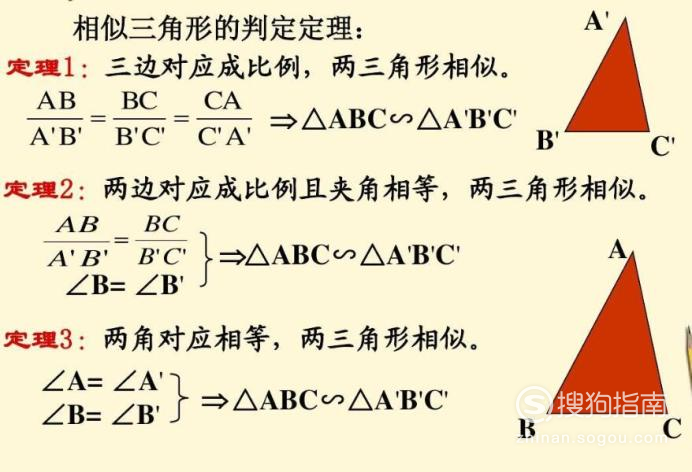
相似三角形怎么判定 搜狗指南

中考数学几何知识重难点 相似三角形 每日头条

相似知识点总结 相似知识点总结精选八篇 范文118

罗斯定理 维基百科 自由的百科全书

勾股定理應用2特殊直角三角形的勾股定理比例 Youtube

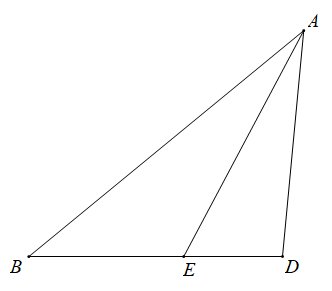
三角形内线段比例定理

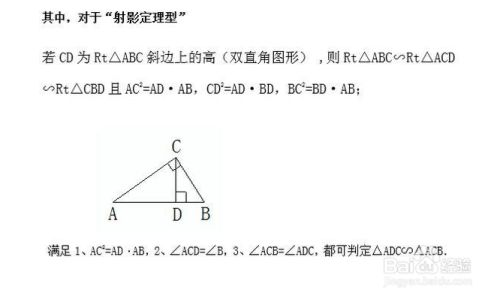
初中数学直角三角形射影定理公式 尚书坊

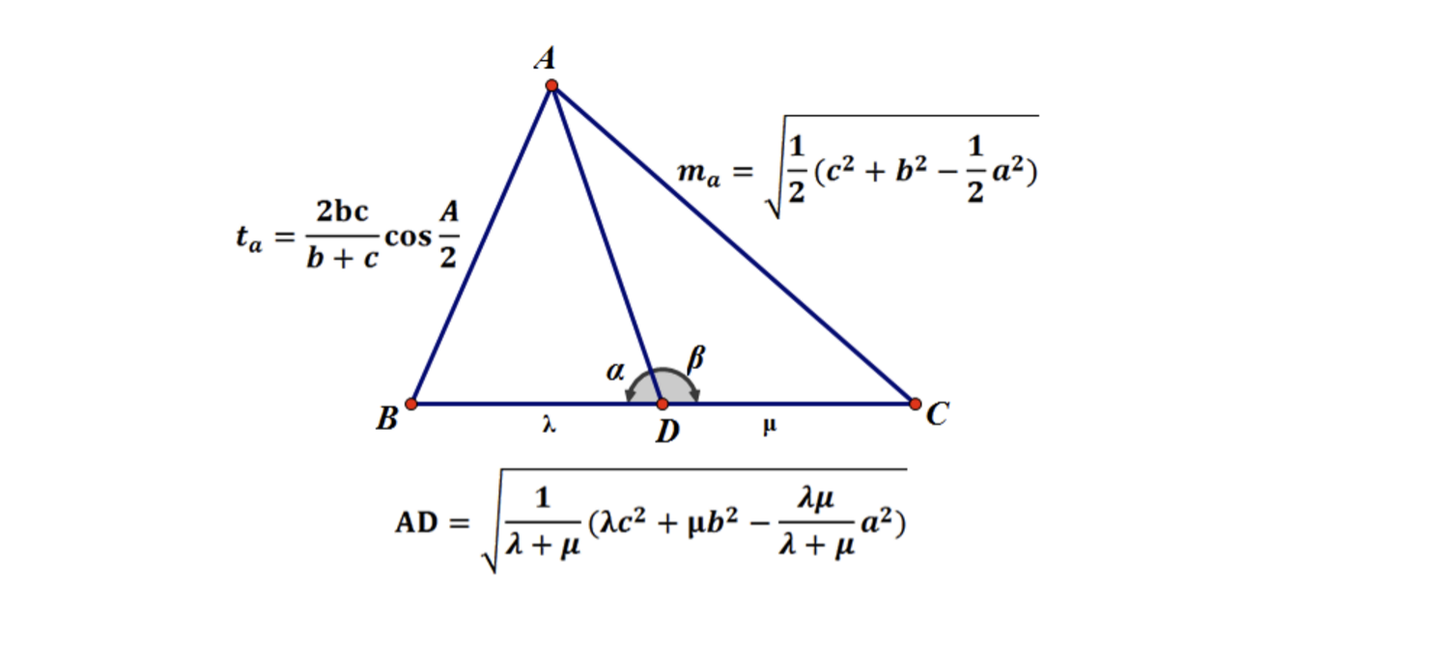
三角形中的线段 知乎

三角形相似的判定方法 百度经验

在相似三角形中 如何添加辅助线 知乎

三角形共边定理 西瓜视频搜索

都江堰南实 教你如何判定三角形相似

相似三角形判定定理的证明 图形的相似ppt下载 牛二ppt

比例中项与射影定理

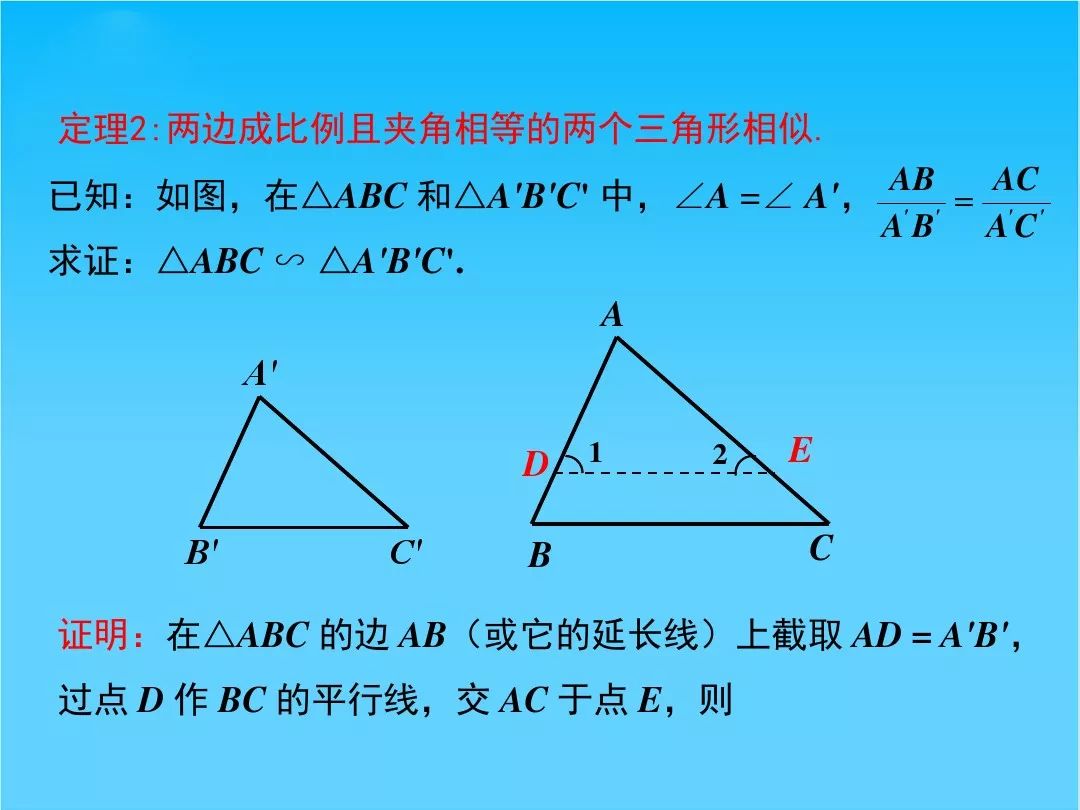
两边成比例 且夹角相等的两三角形相似 Page16 青岛版九年级数学上册电子课本 教材 教科书 好多电子课本网

相似三角形知识学习归类 学起来真轻松 每日头条

初中数学 相似三角形判定定理证明浅见 来说说你的方法吧 知乎

初中数学相似三角形定理知识点总结 快资讯

相似三角形判定定理 搜狗百科

北师大版九年级上册数学相似三角形的定义及其判定定理同步测试卷 莲山文库

极客数学帮小课堂 相似三角形讲解

初中数学北师大版 相似三角形判定定理的证明 精品优质课ppt课件下载 Ppt 文档铺

Ppt 平行线分线段成比例定理powerpoint Presentation Free Download Id

相似三角形定理 尚书坊

头条文章

思维导图 全面解析初中数学 三角形的性质定理及判定 雪花新闻

射影定理 快懂百科

三角形内线段比例定理

全等三角形的判定 勾股定理的应用 平行线分线段成比例定理 初中数学 学习资料大全 免费学习资源下载

1

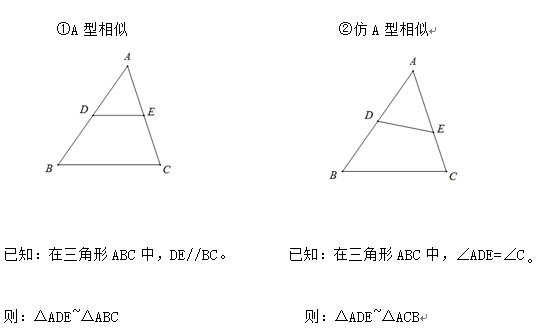
初中数学知识点相似三角形的判定及性质

相似三角形的性质定理 初三网

相似三角形判定定理的证明 图形的相似ppt下载 牛二ppt

四直角三角形的射影定理 人教版高中选修4 1数学电子课本 数九网

怎么证明平行线分线段成比例定理推论 信息阅读欣赏 信息村 K0w0m Com

全等三角形 维基百科 自由的百科全书

初中几何线段 三角形 圆等快速解题高级定理 中考的重点都在这 手机网易网

初中数学直角三角形射影定理记住它解题快捷方便

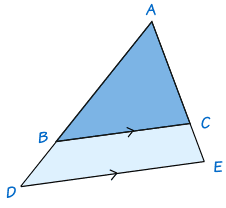
相似三角形定理

Incoming Term: 三角形 比率 定理,