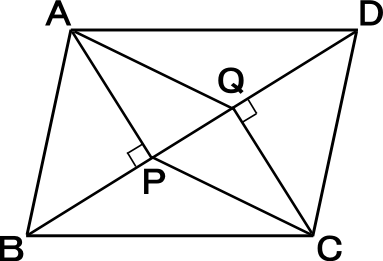
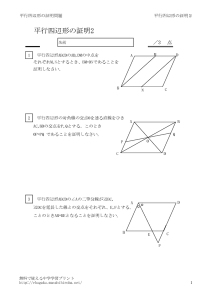
ひし形は平行四辺形なので対角は等しいから ∠abe=∠adf ∠aeb=∠afd=90°(垂線) よって直角三角形で斜辺と一つの鋭角がそれぞれ等しいので abe≡ adf 合同な三角形の対応する辺は等しいのでae=af 2辺が等しいので aefは二等辺三角形である。 abdと acdにおいて 四角形abcdの4辺の中点を図のようにp、q、r、sとするとき、次のことを証明しなさい。 (1)ac=bdのとき四角形pqrsはひし形である。 (2)acとbdが垂直なとき四角形pqrsは長方形である。 この問題の解き方を教えてください2 2組の向かいあう辺が、それぞれ等しい。 abcと cdaで、 ab=cd 1 bc=da 2 ac=ca(共通) 3 1,2,3より3辺がそれぞれ等しいので、
高校入試 英語 数学 学習 三角形と四角形 特別な平行四辺形
平行四辺形 ひし形 証明
平行四辺形 ひし形 証明-平行四辺形の続き 次に,長方形,ひし形,正方形の性質を扱いましょう. 定義 1.4つの角が等しい四角形を長方形という. 2.4辺の長さが等しい四角形をひし形という. 3.4つの角が等しくかつ4辺の長さの等しい四角形を正方形という. まず,長方形(2組の対角の大きさがそれぞれ等しい⑤ $\textcolor{blue}{1}$ 組の対辺が平行でその長さが等しい →定義・性質では出てこないけど、「平行四辺形であること」の証明ではよく使われます。 ①は平行四辺形の 定義 ②、③、④は平行四辺形の
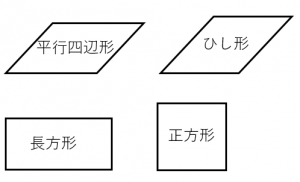



平行四辺形 ひし形 長方形 正方形の違い 具体例で学ぶ数学
四角形の4つの辺の中点を結んでできる四角形 はじめに この問題は,GCにとって,とても重要な問題である特徴を持つ四角形の証明になります 平行四辺形、長方形、ひし形、正方形の特徴を勉強します 更に、平行と面積の関係 四辺形ソケット:標準的に用います 1 特徴 (1)形状が四辺形です (2)体重はソケット後縁の坐骨受けで支持します (3)形状は そもそも、証明する必要がない証明だと思いますが・・・ ひし形は四辺の長さが等しい 四辺の長さが等しいならば 当然、二組の対辺の長さもそれぞれ等しい ゆえにひし形は平行四辺形であ
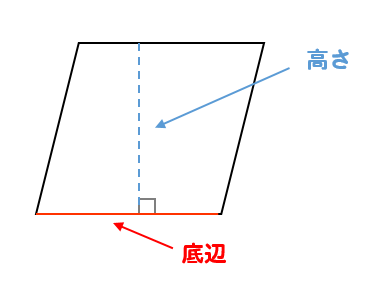
ひし形の面積が『対角線×対角線÷2』となる理由 考え方としては\(2\)つあります。 理由1対角線を底辺とした平行四辺形に変形できる ひし形を変形することで、一方の対角線を底辺とする平行四辺形にすることができます。その時の高さはもう一方のひし形であることを証明する問題 図において長方形abcdの辺ab,bc,cd,daの中点をそれぞれe,f,g,hとする。 四角形efghは、ひし形であることを証明せよ。 長方形であることを証明する問題 下の図において平行四辺形abcdの辺adの中点をmとするとき 、mb=mcならば、/平行四辺形になる条件/平行四辺形になることの証明/ 対角線に注目/ 三角形の合同を先に証明/いろいろな四角形/面積が等しい三角形/ 面積を求める /等積変形/FdData 中間期末製品版のご案内 FdData 中間期末ホームページ 掲載のpdf ファイル(サンプル)一覧 ※次のリンクはShiftキー
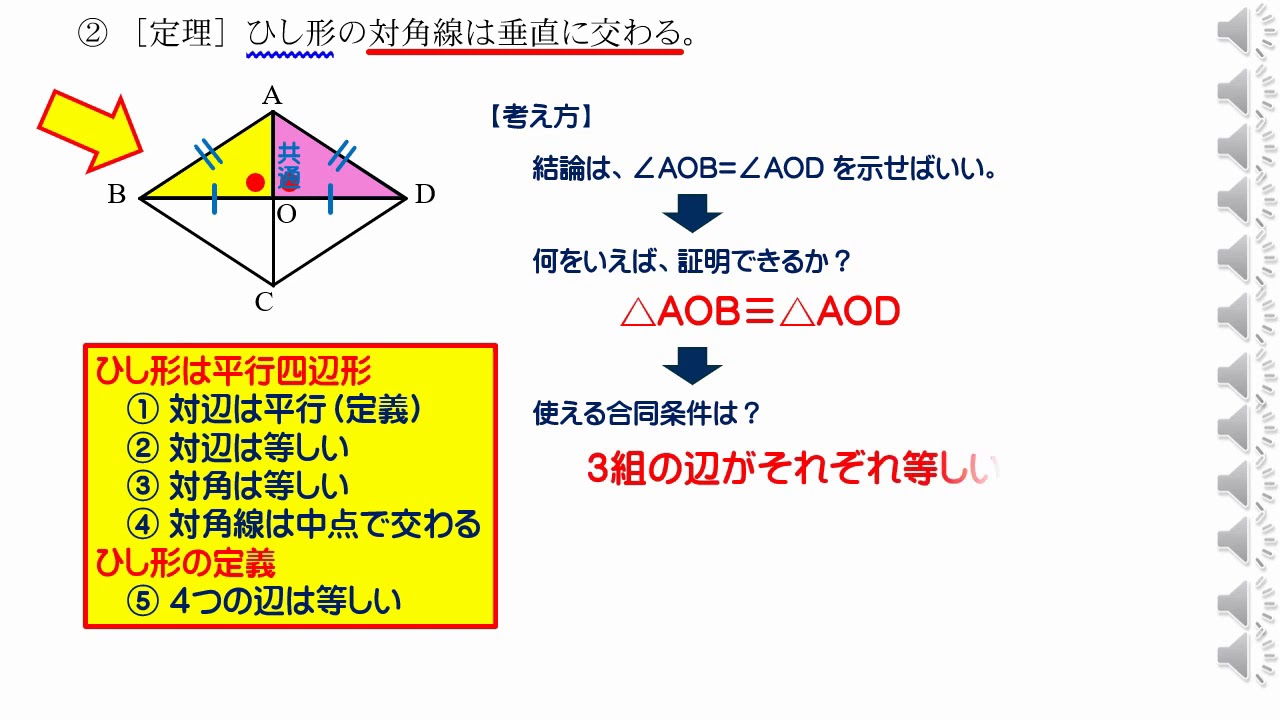
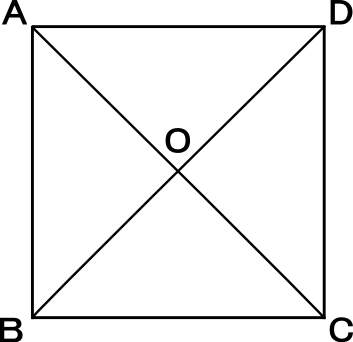
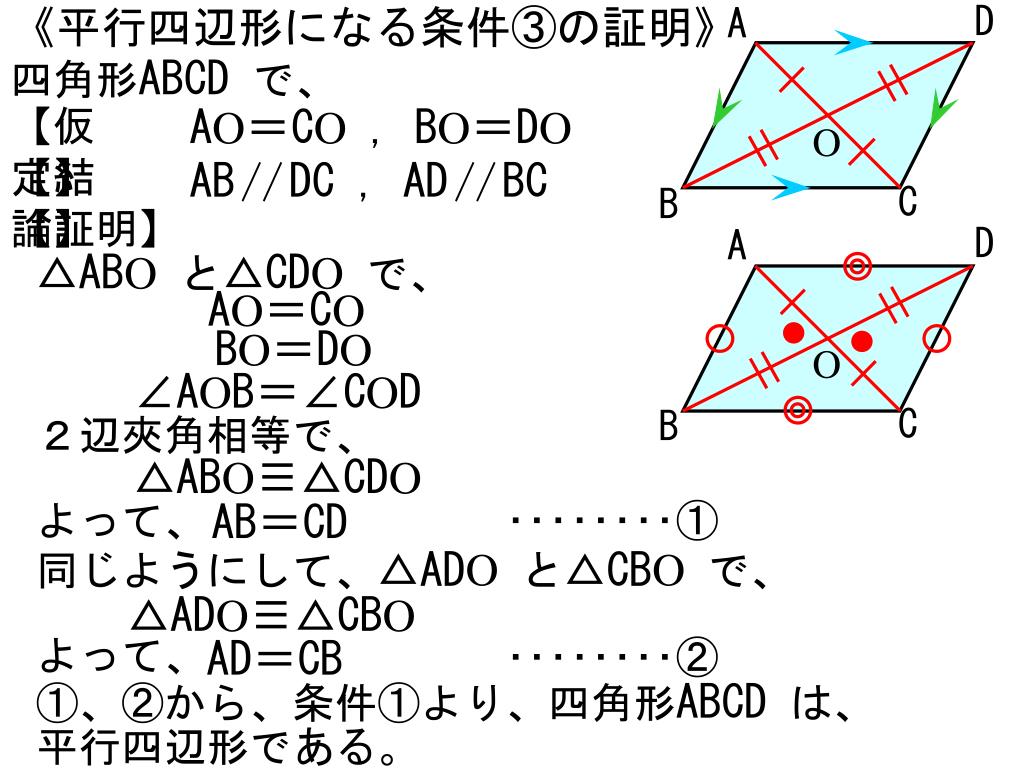
4つの辺がすべて等しい四角形 特別を平行四辺形の性質 ・ 大方形の 2 つの対角線の長さは等しい。 ・ ひし形の 2 つの対角線は垂直に交わる。ひし形は平行四辺形なので bo=do 2 ao=ao(共通) 3 1、2、3より3辺がそれぞれ等しく abo≡ ado ∠aob=∠aod よって ao⊥bd <戻る> 長方形 対角線の長さが等しく、それぞれの中点で交わるとき長方形になる。 証明 それぞれの中点で交わるので四角形abcdは平行四辺形になる。 abcと dcbで 平行証明することができる。 ・平行四辺形になるための条件を,記号を用 いて表したり,その意味を読み取ったりす ることができる。 ・平行四辺形になるための条件を理解してい る。 課題プリント 定期テスト 15 16 特別な ・長方形やひし形,正方形 平行四辺形
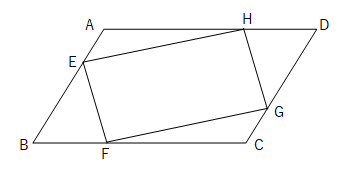



中2数学 平行四辺形の証明のポイントと練習問題 Examee
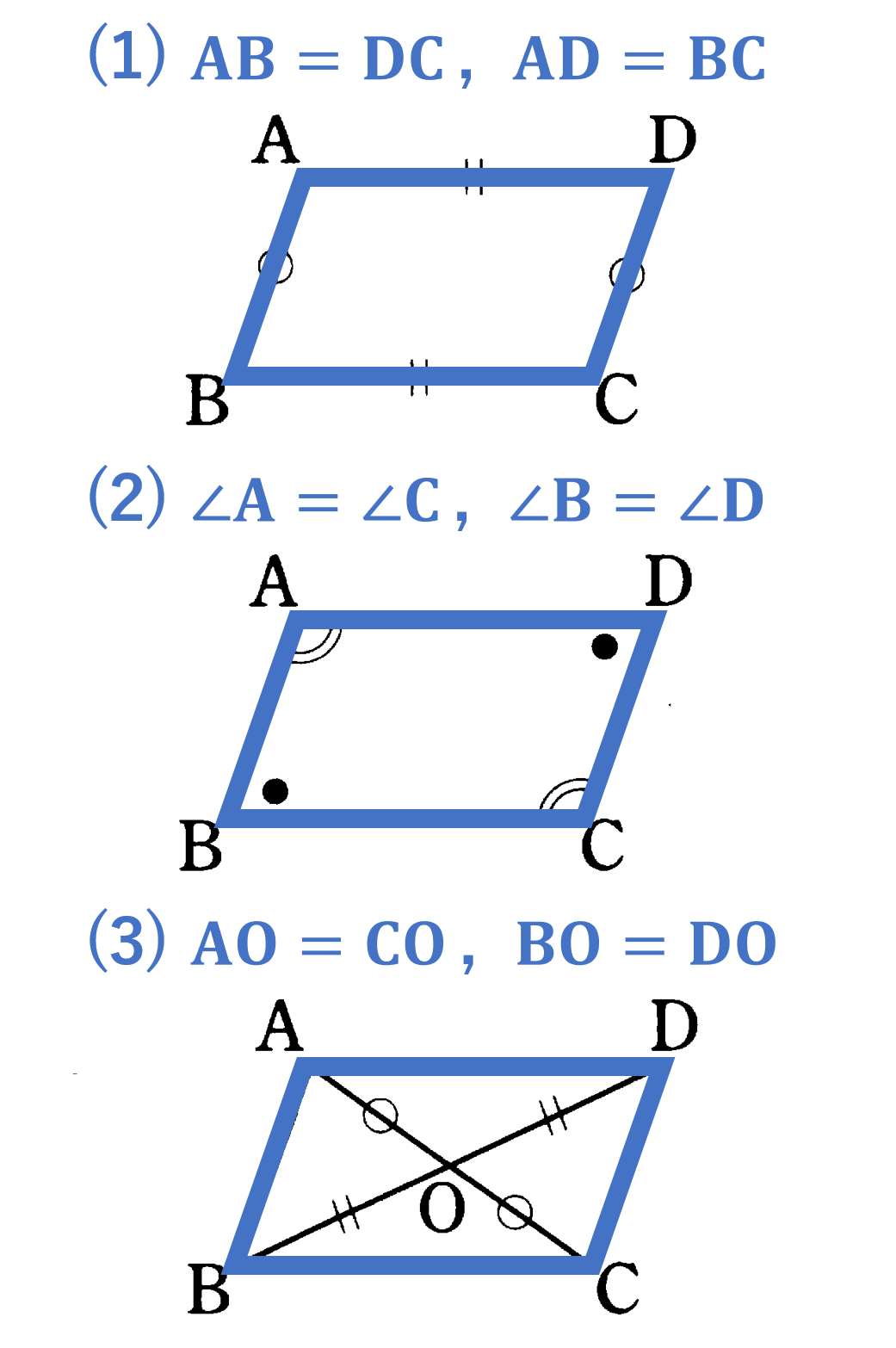



最高のコレクション ひし形 の 定理 シモネタ
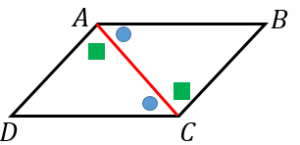
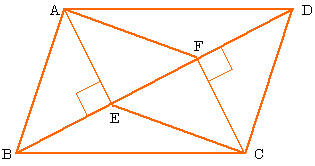
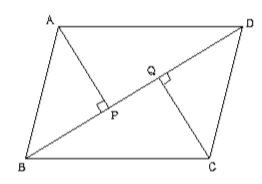
実際にかいた平行四辺形 a d b f c e 平行四辺形 成り立たない 成り立たない 成り立ちそう 長方形 ひし形 a d b f c e 予想 四角形abcdがひし形ならば,af=ceになる。 a d b f c a d c b f e どのように証明すればよいのかな。 四角形abcdを平行四辺形に変えたときも,af=ceになるといってよいでしょうか平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質 平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを 中2数学 基本解説 問題 233 平行四辺形3 長方形とひし形 プリント 平行四辺形abcdの対角線を 関心・意欲・態度 ・垂直,平行や台形,平行四辺形,ひし形 平行四辺形の証明問題をマスターしていこう! 演習問題で理解を深める! 平行四辺形abcdの頂点a、cから対角線bdに垂線をひき、対角線との交点をそれぞれe、fとする。このときae=cfとなることを証明しなさい。 解説&答えはこちら <証明> abeと cdfにおいて 仮定より ∠aeb=∠cfd=90° ① 平行



証明の問題です 平行四辺形abcdにおいて対角線bdが角bを Yahoo 知恵袋




答えがこうらしいのですが 4行目の角agf 角cgf 90 の Clear
など スポンサーリンク 代表的な証明パターン練習問題1 練習問題の解答1 ABDと CBDにおいて 仮定より AB=CB① 共通な辺より BD=BD③ (BDは共通でも) ①②③より、2組の辺とその間の角がそれぞれの等しいので・ 長方形、ひし形、正方形には、平行四辺形の性質があることに関心をもち、それぞれ の性質についてまとめようとする。 ・ 長方形、ひし形、正方形が平行四辺形の特別な場合であるとみることができる。 段階 学習活動数学的活動を通した指導のポイント つかむ ・平行四辺形になる仮定と結論,逆,合同条件/三角形の合同の証明/二等辺三角形の定理/ 二等辺三角形の性質を使った証明 /二等辺三角形になることを証明/正三角形/ 直角三角形/ 平行四辺形の性質/平行四辺形になるための条件/長方形・ひし形・正方形/ 折り返し /平行線と面積/FdData 入試製品版



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




78右の図の平行四辺形 Abcd で 辺 Cd 上に点e を 0 A D クァンダ Qanda で解き方を見る
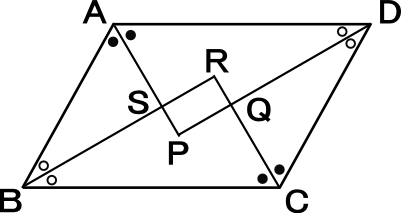
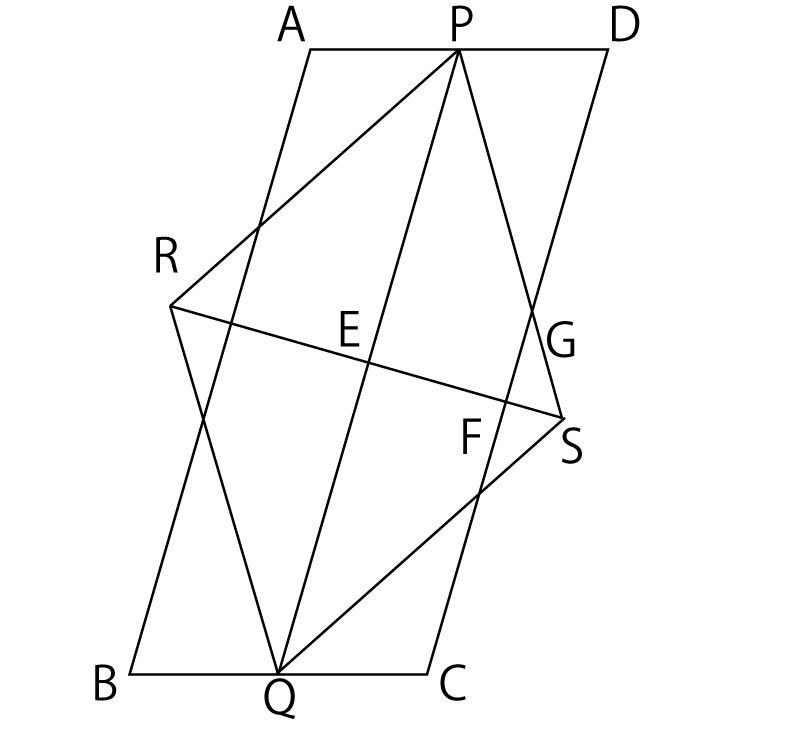
ひし形(平行四辺形の一種)prqsの平行な2組の対辺のうち、rq∥psが目的三角形の辺と重なっていることに気がつくと、平行線の錯角・同位角の関係が使えそうである。 まず、平行線の錯角・同位角、そして対頂角のことを整理しておこう。 注目する2つの平行線を図に描きいれる。 する至急ひし形は平行四辺形である の証明を教えてください そもそも、証明する必要がない証明だと思いますが・・・ひし形は四辺の長さが等しい四辺の長さが等しいならば当然、二組の対辺の長さもそれぞれ等しいゆえに abcでabの中点をm acの中点をnとする mnの延長上にmn=ndとなる点dを数学25章図形の性質と証明「平行四辺形の性質」<基本問題①> 組 番 名前 次の図を作図しなさい。 (1)平行四辺形ABCDを三角定規を使ってかきなさい。 (2)長方形ABCDを三角定規とコンパスを使って作図しなさい。 (3)2つの対角線がそれぞれAC=4cm,BD=6cmの平行四辺形ABCDを定規(も



Www Tsumugi Ne Jp Member Data Sm2 5 Sm2 5 4 Pdf



四角形の性質 ひし形の性質 平行四辺形の性質 正方形の性質 長方形の性質 女子学院中学 05年 平成17年度 入試算数問題 まいにち一題 中学受験過去問題研究
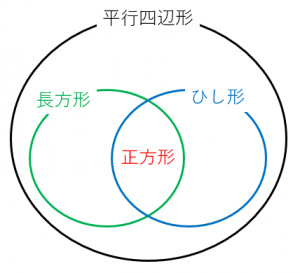
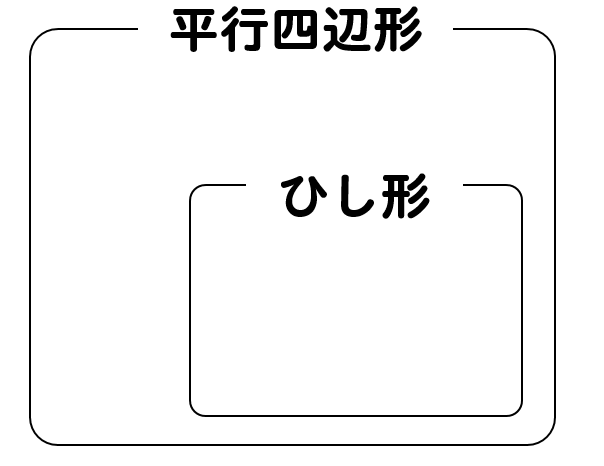
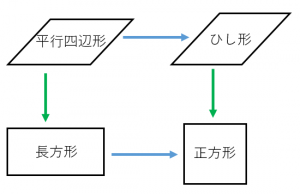
1.その他の平行四辺形 長方形、ひし形、正方形は平行四辺形の定義に当てはまるので平行四辺形のなかまです。 ★定義 長方形・・・\(4\)つの角が等しい四角形 ひし形・・・\(4\)辺が等しい四角形 正方形・・・\(4\)つの角が等しく、\(4\)辺が等しい四角形長方形,ひし形,正方形は,平行四辺形の一種と見ることができる。 4.実践を終えて(問題点と改善策) 授業をしてみて感じたこと,研究協議で議論されたこと,指導助言いただいたことをまとめてみる。 《問題点1》図をかくことが生徒には困難 ・ 1つの図をかくために,正三角形を3つかく(証明) 2.ひし形の対角線は垂直に交わる。(証明) 3.正方形の対角線の長さは等しく、垂直に交わる。 図形を選び、頂点をドラッグして、対角線がどういう条件のとき長方形やひし形になるか調べよう ;




中2数学 平行四辺形の証明 練習編 映像授業のtry It トライイット
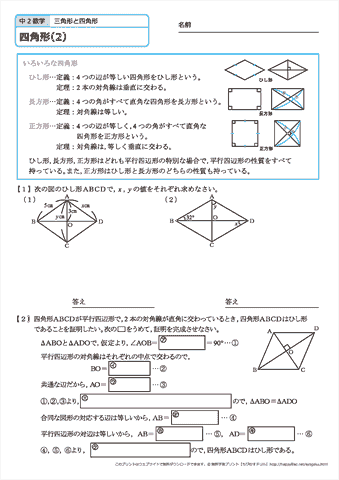



中学2年生 数学 四角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
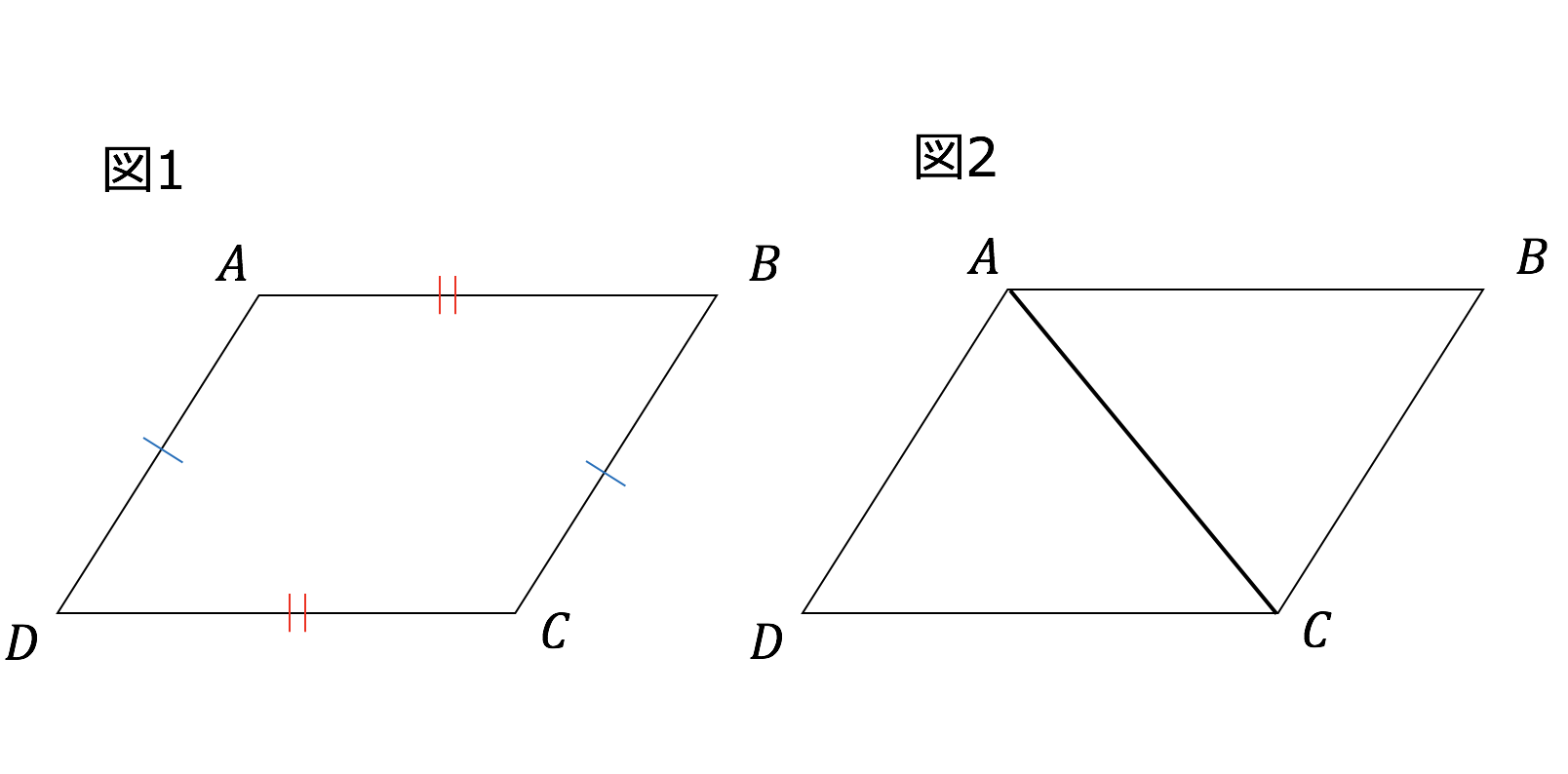
※ この問題では「向かい合う1組の辺が平行でかつ長さが等しい → 平行四辺形」という定理を使ったが,「2組の向かい合う辺がそれぞれ平行 → 平行四辺形」という定理を使って証明するときは,次の(A)のように書けばよい.また,「2組の向かい合う辺の長さがそれぞれ等しい → 平行四辺形ひし形abcdは平行四辺形である。 まとめ 長方形やひし形や正方形は平行四辺形の仲間である。 長方形やひし形の対角線の性質を調べます。 〔長方形の対角線の性質〕長方形の対角線は(それぞれの中点で交わり)等しい。 〔証明〕長方形abcdの対角線acとdbをひく。 abcと ( )において 長方形の定義平行四辺形の場合の証明を振り返ることにより,四角形の包摂関係について考えることも大切である。 本アイディア例のように,特殊から一般へと発展的に考えることは,第3学年において学習する円周 角の定理の証明や三平方の定理の証明などでも大切である。 参照 「平成27年度 報告書 中



1




平行四辺形の性質 と ひし形の性質 を比べる とちぎeライブラリ
平行四辺形とひし形の違いってなに??←今回の記事 平行四辺形の角度、辺の長さを求める問題を解説! 平行四辺形の中から面積の等しい三角形を見つける問題を徹底解説! 等積変形三角形の面積問題と作図のやり方は?証明問題も紹介!平行四辺形の性質で角度を求めたり、平行四辺形であることを証明したりする問題がよく出されます。 このような問題を解くには平行四辺形の定義や性質をきちんと抑えておく必要があるので、ぜひ今回の内容を参考にしてください。 目次 平行四辺形の定義と性質 平行四辺形の性質の証明下の図は特別な平行四辺形をまとめたものです。それぞれの にあてはまる語をいれて、 文章を完成させなさい。 2 下の図は、四辺形をまとめたものです。①から⑤にあてはまる四角形の名称を答えなさい。 ① ② ③ ④ ⑤ 図形の性質と証明⑨いろいろな四角形A 学 年 2年 学習日: 月 日



Www1 Iwate School Jp Action Common Download Main Upload Id 1336



平行四辺形 ひし形 長方形 正方形の違い 具体例で学ぶ数学
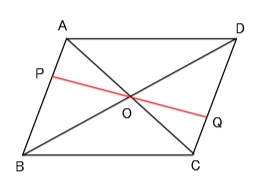
平行四辺形であることを証明する問題 問題2 四角形abcdの対角線の交点をoとする。 これから紹介する成立条件の中で どれか1つでも当てはまっている四角形は平行四辺形になります。 3分で分かる!平行四辺形とは?定義や性質・成立条件をわかりやすく 👋 平行四辺形の成立条件その4:2台形,平行四辺形,ひし形の対角線の長さは等しいとは限りません.他は図のように等しくなります. →閉じる← 4. 対角線はそれぞれの頂角を2等分する.1組の等しい対辺の長さをa、他の辺をb、cとし、1組の等しい対角の大きさをθとしますと、余弦定理から、対角線について次の関係が得



中2数学 発展問題 平行四辺形3 長方形とひと形 問題 233 プリント




中学校数学 証明のコツ 四角形の性質




中学校数学 証明のコツ 四角形の性質




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット



平行四辺形の3つの性質とその証明 具体例で学ぶ数学




平行四辺形 ひし形 長方形 正方形の違い 具体例で学ぶ数学



至急 ひし形は平行四辺形である の証明を教えてください そもそ Yahoo 知恵袋




2 1の授業と 総復習 得点力 数学 受験ブログ



平行四辺形とひし形の違いってなに それぞれの特徴を比較 数スタ




勉強しよう数学 ひし形の対角線の直交の公式と2重平行四辺形の面積の公式




至急 1問でもいいので教えて下さい よろしくお願いします Clear
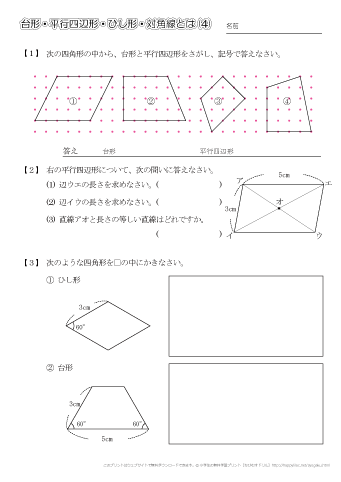



小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生




3分でわかる ひし形 菱形 の定義 Qikeru 学びを楽しくわかりやすく
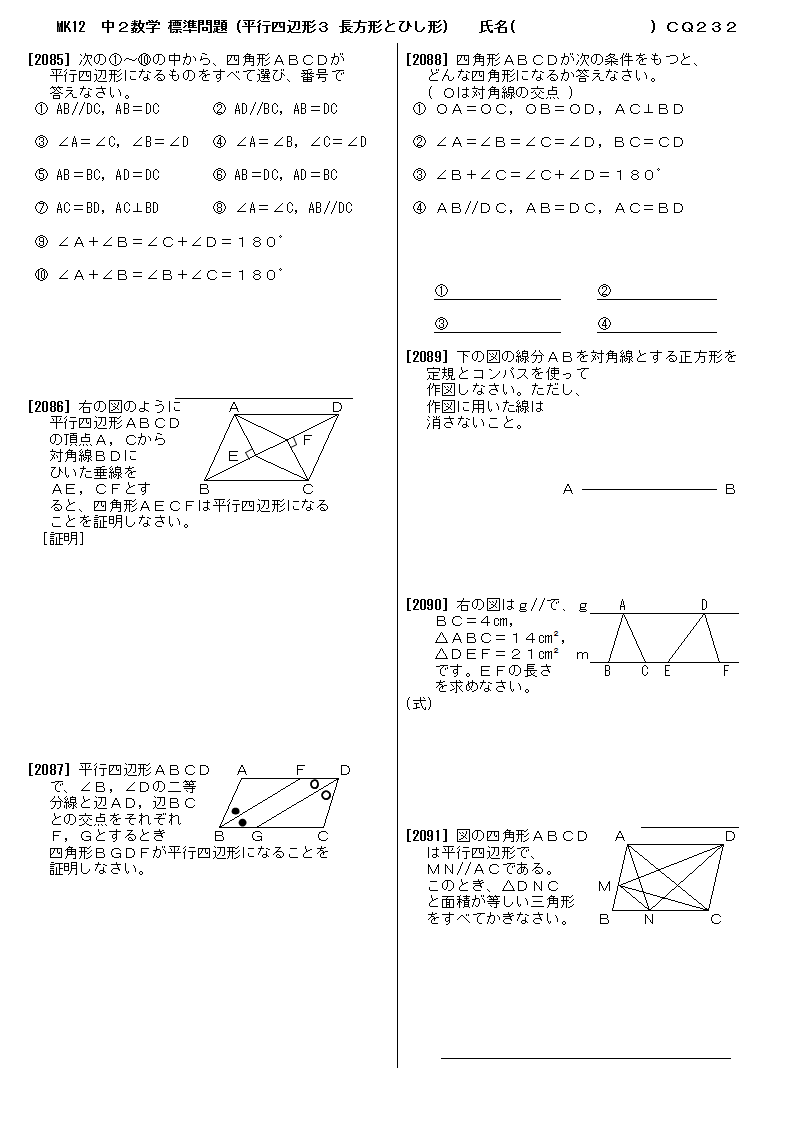



無料 中2数学 標準問題 問題プリント 232 平行四辺形3 長方形とひし形




中学数学 特別な平行四辺形について Clear
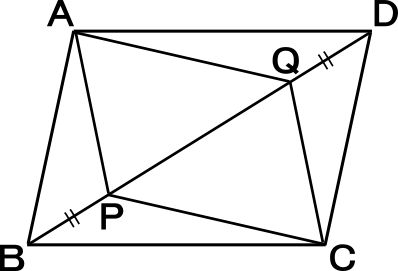



中学2年数学練習問題 平行四辺形になる条件と証明方法 図形と合同
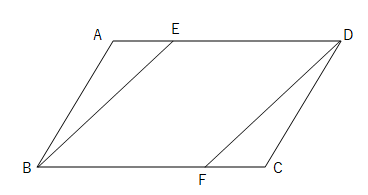



中2数学 平行四辺形の証明のポイントと練習問題 Examee




3分でわかる ひし形 菱形 の定義 Qikeru 学びを楽しくわかりやすく
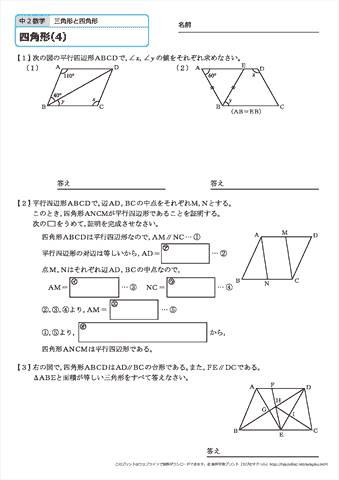



中学2年生 数学 四角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




台形と平行四辺形を平行な辺の組の数で分類することは 原理的に不可能である 小学校4年生の算数 身勝手な主張



高校入試 英語 数学 学習 三角形と四角形 特別な平行四辺形



中学校数学についてです 中二の四角形の証明なのですが 画像の青く印をつけた所が Yahoo 知恵袋




平行四辺形になるための条件 Youtube




平行四辺形とひし形の違いってなに それぞれの特徴を比較 数スタ




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学
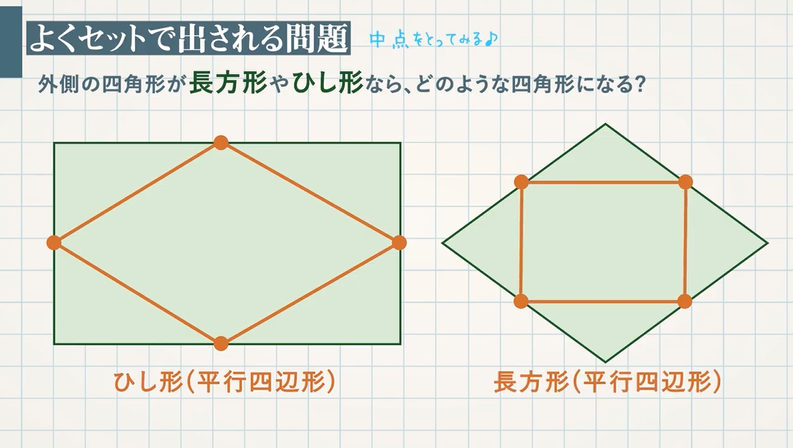



中点連結定理を使った平行四辺形であることの証明 教遊者



1



Http Www C Able Ne Jp Sa Kun Kadai K 06 Pdf
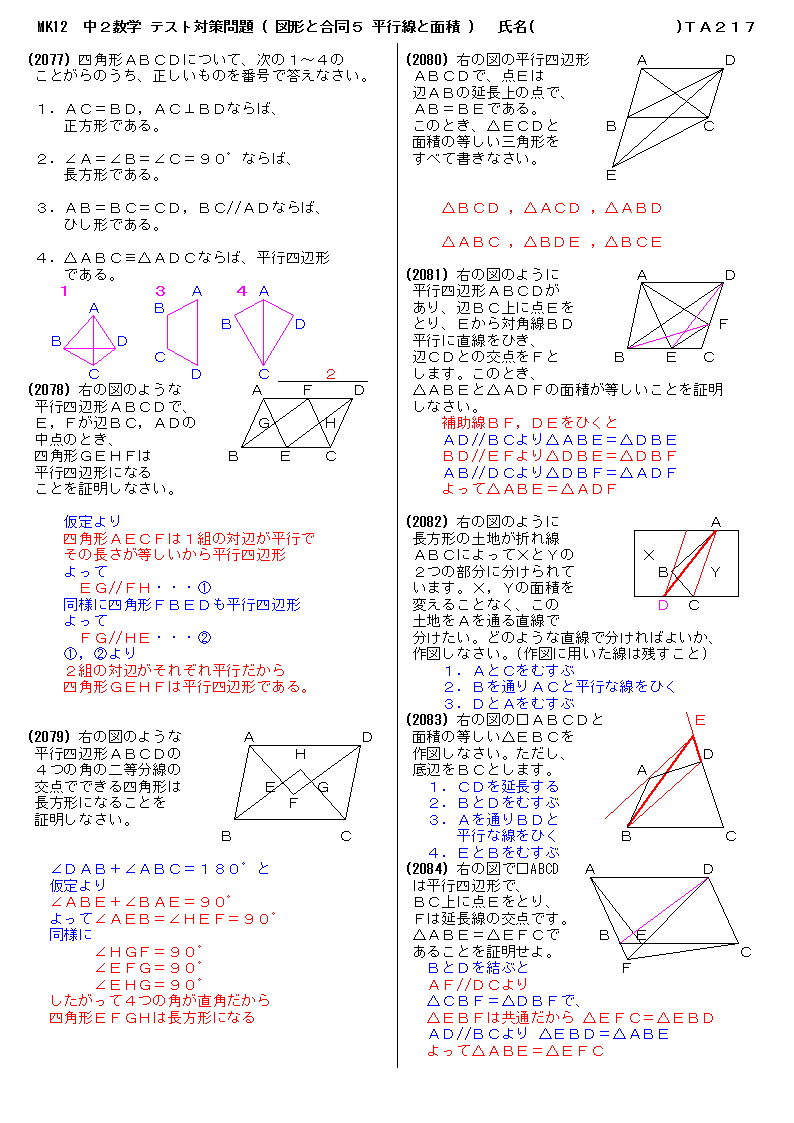



無料 中2数学 テスト対策 解答プリント 217 図形と合同5 平行線と面積




数学 中2 74 平行四辺形になる条件 Youtube




無料 中2数学 標準問題 解答プリント 232 平行四辺形3 長方形とひし形



3




条件は長方形 ひし形 正方形 全部当てはまってるから3つじゃないんですか なんでひし Clear




平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を押さえよう 遊ぶ数学




四角形 Ict教材eboard イーボード




ひし形の性質 対角線はなぜ垂直に交わるのか Qikeru 学びを楽しくわかりやすく



1




78 Abcd Cd E D Lihat Cara Penyelesaian Di Qanda




高校数学b ベクトルの成分表示と平行四辺形 受験の月




小5算数 平行四辺形が描けると 角の大きさがわかる ブログ アビット




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット



特別な平行四辺形2



四角形 ひし形 平行四辺形 台形 の書き方 作図 まとめ 受験辞典




平行四辺形 中学数学で遊ぶ 身勝手な主張
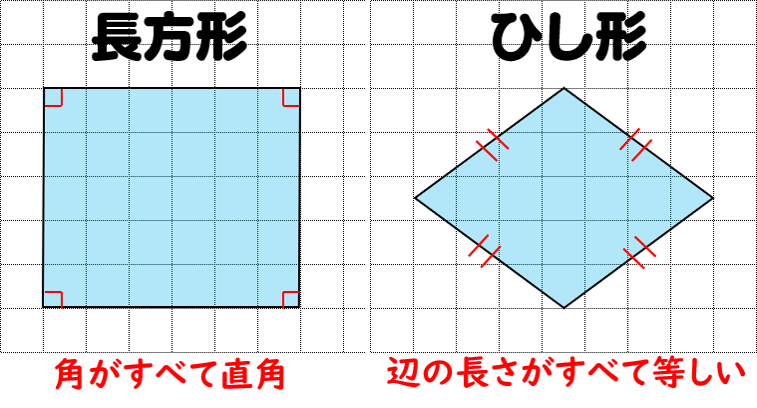



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun
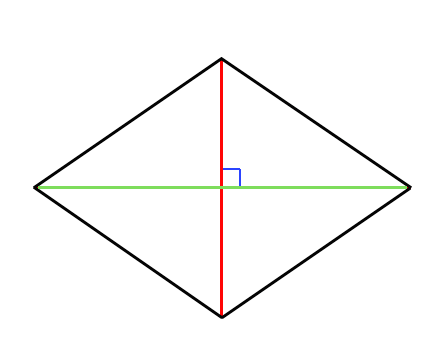



平行四辺形と長方形 ひし形 正方形の関係 苦手な数学を簡単に



特別な平行四辺形 チーム エン



Www Tsumugi Ne Jp Member Data Sm2 5 Sm2 5 4 Pdf
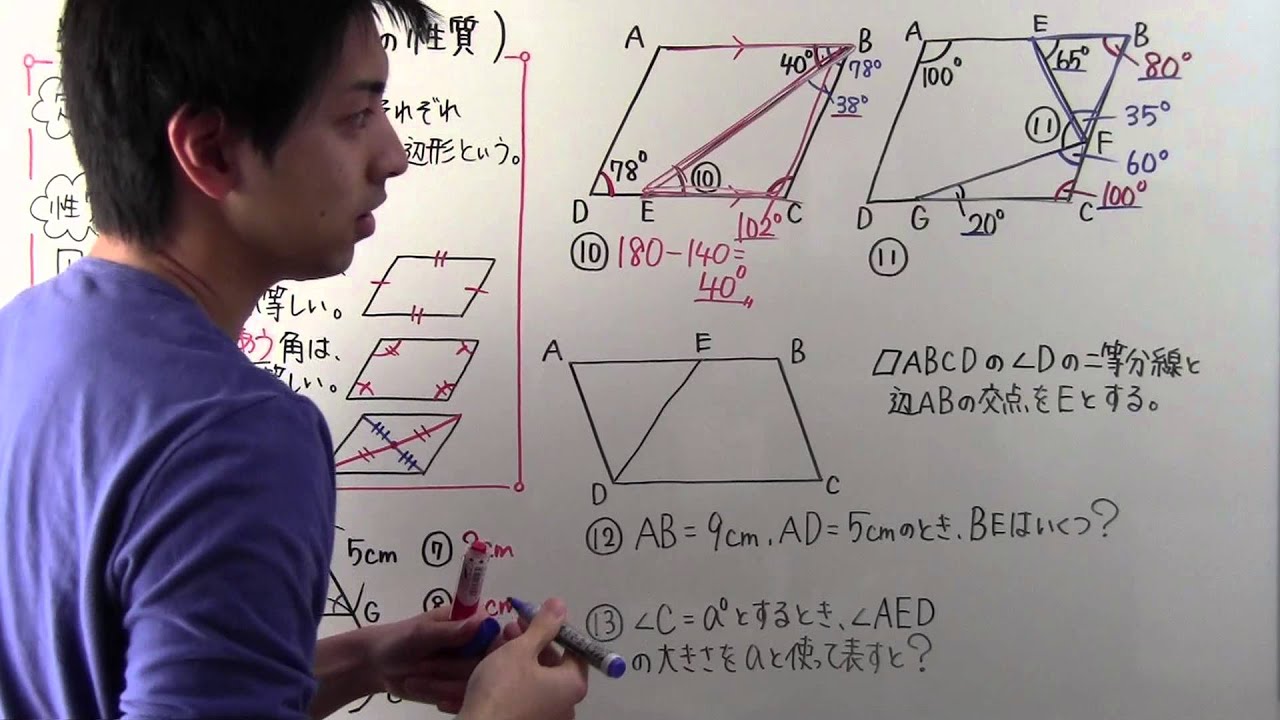



数学 中2 73 平行四辺形の性質 Youtube



中2数学 基本問題 問題 233 平行四辺形3 長方形とひし形 プリント



Hello School 数学 問題集 ハロ数 中2 四角形



中2数学 平行四辺形の証明のポイントと練習問題 Examee
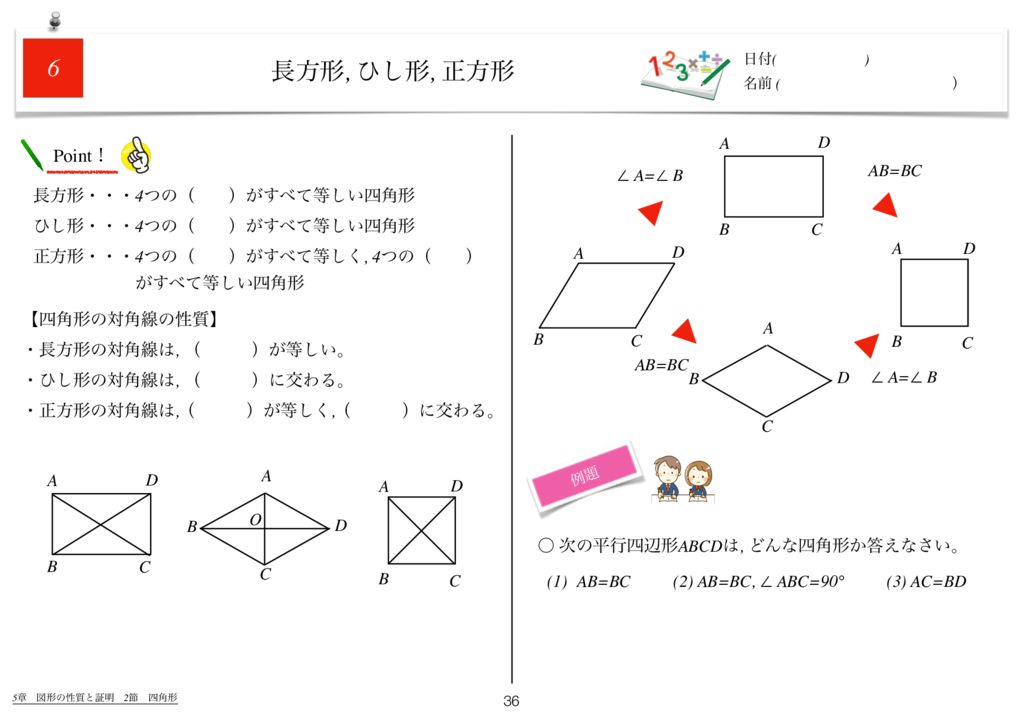



世界一わかりやすい数学問題集中2 5章 図形の性質と証明



高校入試 英語 数学 学習 三角形と四角形 特別な平行四辺形




至急 1問でもいいので教えて下さい よろしくお願いします Clear



中点連結定理を使った平行四辺形であることの証明 教遊者
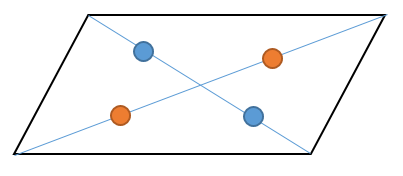



小学算数 平行四辺形 ひし形 長方形 正方形の対角線は真ん中で交わる 偏差値40プログラマー



3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ



特別な平行四辺形 Youtube



19年前期 千葉県公立高校入試 数学 第4問 図形の証明 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



特別な平行四辺形2



中学2年数学練習問題 平行四辺形 長方形 ひし形 正方形 の性質




中学校数学 証明のコツ 年01月



中学2年数学練習問題 平行四辺形 長方形 ひし形 正方形 の証明



ひし形の定義は 1分でわかる定義 正方形 平行四辺形との違い 対角線との関係




平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は4つ 中学や高校の数学の計算問題




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット



特別な平行四辺形2



中2数学 平行四辺形の証明のポイントと練習問題 Examee



四角形の4つの辺の中点を結んでできる四角形




四角形 Ict教材eboard イーボード



中学2年数学練習問題 平行四辺形になる条件と証明方法 図形と合同



至急 ひし形は平行四辺形である の証明を教えてください そもそ Yahoo 知恵袋



平行四辺形とひし形の違いってなに それぞれの特徴を比較 数スタ




平行四辺形であることを証明する 苦手な数学を簡単に




画像をダウンロード 平行 四辺 形 特徴 ニスヌーピー 壁紙




中点連結定理を利用した証明 チーム エン



Ppt 5 図形と合同 Powerpoint Presentation Free Download Id



平行四辺形とひし形の違いってなに それぞれの特徴を比較 数スタ



Katekyo学院山形 中学生 証明問題 21 1 27



平行四辺形 ひし形 長方形 正方形の違い 具体例で学ぶ数学



長方形とひし形



19年前期 千葉県公立高校入試 数学 第4問 図形の証明 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット




中2数学 長方形 ひし形 正方形 映像授業のtry It トライイット




平行四辺形の性質 と ひし形の性質 を比べる とちぎeライブラリ




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



0 件のコメント:
コメントを投稿